JTS CBS Kütüphanesi Rehberi 4 - Delaunay Üçgenleme, Voronoi Diyagram, Convex Hull

 Previously on JTS

1.  JTS CBS Kütüphanesi Rehberi  1 - Geometri Modeli
2.  JTS CBS Kütüphanesi Rehberi  2 - Geometrik İlişki Hesaplamaları 
3.  JTS CBS Kütüphanesi Rehberi  3 - Geometrik Alan Hesaplamaları

Merhabalar. JTS (Java Topology Suite) rehberimizin önceki bölümlerinde geometri modellerini tanımış, geometrilerin birbiri ile ilişkilerini incelemiş, daha sonra ise geometrik alan hesaplamaları üzerinde durmuştuk. Bu bölümde ise Delaunay Triangulation üçgenleme algoritması ile nasıl üçgenler oluşturulacağını, Voronoi diyagramı üretmeyi ve convex hull poligonu üretimini göreceğiz. Tüm görselleştirme örnek kodlarına GitHub'da şuradan ulaşabileceğinizi hatırlatarak başlayalım. 

Delaunay Triangulation / Üçgenleme

Delaunay triangulation / üçgenleme algoritması, bir nokta setinden anlamlı üçgenler oluşturma yöntemidir. Yüzey modelleme, (terrain modelling), mesh üretme ve rota planlama gibi alanlarda kullanılabilmektedir. Biz örneğimizde rastgele koordinatlardan oluşan bir nokta seti oluşturup JTS'den DelaunayTriangulationBuilder sınıfını kullanarak bu noktalardan bize üçgenler üretmesini isteyeceğiz. Nokta sayısını 100 ve 1000 yaparak iki defa çalıştırıp çıkan sonuçları görselleştireceğiz. Örnek projemizdeki DelaunayUcgenleme.java sınıfını çalıştırarak görselleştirebilirsiniz.

GeometryFactory geometryFactory = new GeometryFactory();

Random randomX = new Random(System.currentTimeMillis());

Random randomY = new Random(System.currentTimeMillis() + 100);

List<Coordinate> coords = new ArrayList<>();

int noktaSayisi = 100;

for(int i = 1; i <= noktaSayisi; i++) {
   
	int xRandomlySelected = randomX.nextInt(405) + 25;
   
	int yRandomlySelected = randomY.nextInt(405) + 20;
   
	System.out.println(i + ". Rastgele secilen nokta " + xRandomlySelected + ", " + yRandomlySelected);

	coords.add(new Coordinate(xRandomlySelected, yRandomlySelected));

}

DelaunayTriangulationBuilder ucgenBuilder = new DelaunayTriangulationBuilder();

ucgenBuilder.setSites(coords);

Geometry triangles = ucgenBuilder.getTriangles(geometryFactory);

List<Polygon> uretilenUcgenler = new ArrayList<>();

if(triangles instanceof GeometryCollection) {
   
	GeometryCollection geometryCollection = (GeometryCollection) triangles;
   
	System.out.println("Üretilen üçgen sayısı: " + geometryCollection.getNumGeometries());
   
	for(int i = 0; i < geometryCollection.getNumGeometries(); i++) {
	   
		Polygon ucgen = (Polygon) geometryCollection.getGeometryN(i);
	   
		uretilenUcgenler.add(ucgen);
	}
   
}

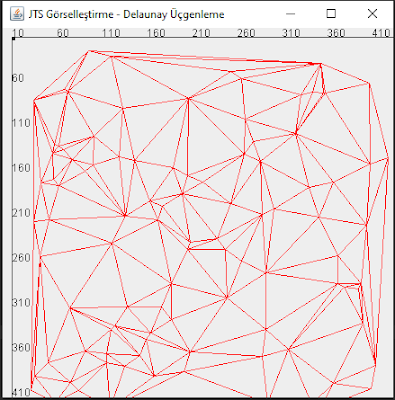Delaunay triangulation / üçgenleme

Nokta sayısını 1000 yaparsak aşağıdaki gibi bir çizimle karşılaşıyoruz.

Delaunay triangulation / üçgenleme noktalar

Voronoi Diagram / Diyagram

Matematikte, bir Voronoi diyagramı, bir düzlemin belirli bir nesne kümesinin her birine yakın bölgelere bölünmesidir. En basitinden, bu nesneler düzlemdeki sonlu sayıda noktadır (tohumlar, siteler veya oluşturucular olarak adlandırılır). Her tohum için, o tohuma diğerlerinden daha yakın olan düzlemin tüm noktalarından oluşan, Voronoi hücresi (Voronoi cell) adı verilen bir bölge vardır. Biyolojiden kimyaya, sağlıktan mühendisliğe çok çeşitli kullanım alanları mevut.

Üçgenleme örneğimize benzer şekilde rastgele 100 noktadan VoronoiDiagramBuilder sınıfını kullanarak Voronoi diyagramı oluşturacağız. Örnek projemizdeki VoronoiDiagramGorsellestirme.java sınıfını çalıştırarak görselleştirebilirsiniz.

GeometryFactory geometryFactory = new GeometryFactory();

Random randomX = new Random(System.currentTimeMillis());

Random randomY = new Random(System.currentTimeMillis() + 100);

List<Coordinate> coords = new ArrayList<>();

int noktaSayisi = 100;

for(int i = 1; i <= noktaSayisi; i++) {
	
	int xRandomlySelected = randomX.nextInt(250) + 65;
	
	int yRandomlySelected = randomY.nextInt(250) + 50;
	
	System.out.println(i + ". Rastgele secilen nokta " + xRandomlySelected + ", " + yRandomlySelected);

	coords.add(new Coordinate(xRandomlySelected, yRandomlySelected));

}

VoronoiDiagramBuilder diagramBuilder = new VoronoiDiagramBuilder();

diagramBuilder.setSites(coords);

Geometry triangles = diagramBuilder.getDiagram(geometryFactory);

List<Polygon> uretilenPoligonlar = new ArrayList<>();

if(triangles instanceof GeometryCollection) {
	
	GeometryCollection geometryCollection = (GeometryCollection) triangles;
	
	System.out.println("Üretilen poligon sayısı: " + geometryCollection.getNumGeometries());
	
	for(int i = 0; i < geometryCollection.getNumGeometries(); i++) {
		
		Polygon poligon = (Polygon) geometryCollection.getGeometryN(i);
		
		uretilenPoligonlar.add(poligon);
	}
	
}

 

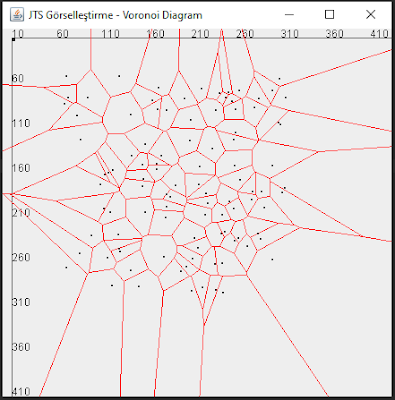Voronoi Diagram / Diyagram

Convex Hull - Dışbükey Örtü, Zarf

Convex hull, bir geometrinin tüm noktalarını kapsayan en küçük poligon olarak tanımlanabilir. Örneğimizde, rastgele tanımladığımız 100 noktadan bir MultiPoint nesnesi oluşturacak ve bu nesnenin convexHull() metodu ile zarf poligonunu üreteceğiz. Örnek projemizdeki ConvexHullGorsellestirme.java sınıfını çalıştırarak görselleştirebilirsiniz.

GeometryFactory geometryFactory = new GeometryFactory();

Random randomX = new Random(System.currentTimeMillis());

Random randomY = new Random(System.currentTimeMillis() + 100);

List<Coordinate> noktaKoordinatlari = new ArrayList<>();

int noktaSayisi = 100;

Point[] noktalar = new Point[noktaSayisi];

for(int i = 1; i <= noktaSayisi; i++) {
   
	int xRandomlySelected = randomX.nextInt(250) + 65;
   
	int yRandomlySelected = randomY.nextInt(250) + 50;
   
	System.out.println(i + ". Rastgele secilen nokta " + xRandomlySelected + ", " + yRandomlySelected);

	Coordinate coordinate = new Coordinate(xRandomlySelected, yRandomlySelected);
   
	noktaKoordinatlari.add(coordinate);

	noktalar[i-1] = geometryFactory.createPoint(coordinate);
}

MultiPoint multiPoint = geometryFactory.createMultiPoint(noktalar);
 
Polygon convexHull = (Polygon) multiPoint.convexHull();

Convex Hull - Zarf

Bu bölümde Delaunay üçgenlemesi ile bir nokta setinden nasıl üçgen üretileceğini, nasıl Voronoi diyagram oluşturulacağını, convex hull poligon geometrisinin nasıl hesaplanacağını gördük. Faydalı olması dileğiyle... 

Önceki Bölümler

1.  JTS CBS Kütüphanesi Rehberi  1 - Geometri Modeli
2.  JTS CBS Kütüphanesi Rehberi  2 - Geometrik İlişki Hesaplamaları 
3.  JTS CBS Kütüphanesi Rehberi  3 - Geometrik Alan Hesaplamaları

Sonraki Bölümler:

JTS CBS Kütüphanesi Rehberi 5 - Quadtree Nedir? Java'da Örnek Kullanım

JTS CBS Kütüphanesi Rehberi  6 - Douglas Peucker Geometri Basitleştirme ve Yoğunlaştırma   

 

Download as E-book PDF